前趋图与程序的执行
# 前趋图与程序的执行
# 序言
在早期未配置Os的系统和单道批处理系统中,程序的执行方式是顺序执行,即在内存中仅装入一道用户程序,由它独占系统中的所有资源,只有在一个用户程序执行完成后,才允许装入另一个程序并执行。可见,这种方式浪费资源、系统运行效率低等缺点。而在多道程序系统中,由于内存中可以同时装入多个程序,使它们共享系统资源,并发执行 显然可以克服上述缺点,程序的这两种执行方式间有着显著的不同,尤其是考虑到程序井发执行时的特征,才导致了在操作系统中引入进程的概念。因此,这里有必要先对程序的顺序和并发执行方式做简单的描述。
# 前趋图
为了能更好地描述程序的顺序和并发执行情况,我们先介绍用于描述程序执行先后颗序的前趋图,所谓前趋图(Precedence Graph),是指一个有向无循环图,可记为DAG(DirectedAcyclic Graph),它用于描述进程之间执行的先后顺序。图中的每个结点可用来表示一个进程或程序段,乃至一条语句,结点间的有向边则表示两个结点之间存在的偏序(Partial Order)或前趋关系(Precedence Relation)。进程(或程序)之间的前趋关系可用“→”来表示。如果进程Pi,和Pj存在着前趋关系,可表示为(Pi, Pj)∈→,也可写成Pi→Pj,表示在Pj开始执行之前Pi必须完成。此时称Pi是Pj的直接前趋,而称Pj是Pi的直接后继。在前趋图中,把没有前趋的结点称为初始结点(Initial Node),把没有后继的结点称为终止结点(Final Node),此外,每个结点还具有一个重量(Weight),用于表示该结点所含有的程序量或程序的执行时间。在图2-1(a)所示的前趋图中,存在着如下前趋关系:
P1→P2, P1→P3, P1→P4, P2→P5,P3→P5,P4→P6,P4→P7,P5→P8,P6→P8,P7→P9,P8→P9
或表示为:
P={P1,P2,P3,P4,P5,P6,P7,P8,P9}
={(P1,P2),{P1,P3}, {P1,P4}, {P2,P5},{P3,P5},{P4,P6},{P4,P7},{P5,P8},{P6,P8},{P7,P9},P8,P9,}
应当注意,前趋图中是不允许有循环的,否则必然会产生不可能实现的前驱关系。如图2-1(b)所示的前驱关系红酒存在着循环。它一方面要求S3开始执行前,S2必须完成,另一方面又要求S2在开始执行前,S3必须完成。显然,这种关系是不可能实现的。
# 程序顺序执行
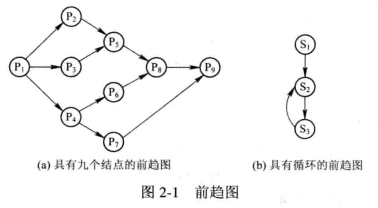
通常,一个应用程序由若干个程序段组成,每一个程序段完成特定的功能,它们在执行时,都需要按照某种先后次序顺序执行,仅当前一程序段执行完后,才运行后一程序段。 例如,在进行计算时,应先运行输入程序,用于输入用户的程序和数据;然后运行计算程序,对所输入的数据进行计算:最后才是运行打印程序,打印计算结果。我们用结点(Node)代表各程序段的操作(在图2-1中用圆圈表示),其中I代表输入操作, C代表计算操作, P为打印操作,用箭头指示操作的先后次序。这样,上述的三个程序段间就存在着这样的前趋关系: Ii→Ci→Pi,其执行的顺序可用前趋图2-2(a)描述。
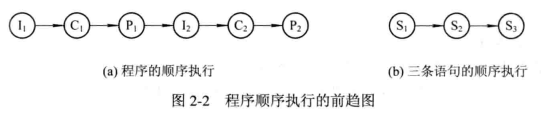
- 即使是一个程序段,也可能存在着执行顺序问题,下面给出一个包含了三条语句的程序段:
S1: a:= x+y
S2: b:=a-5
S3: c:=b+1
其中,语句S2必须在语句S1后(即a被赋值)才能执行,语句S3也只能在b被赋值后才能执行,因此,三条语句存在着这样的前趋关系:S1→S2→S3,应按前趋图2-2(b)所示的顺序执行。
- 所以程序顺序执行时有以下几个特征:
- 顺序性:指处理机严格地按照程序所规定的顺序执行,即每一操作必须在下一个操作开始之前结束。
- 封闭性:指程序在封闭的环境下运行,即程序运行时独占全机资源,资源的状态(除初始状态以外)只有本程序才能改变它,程序一旦开始执行,其执行结果不受外界因素影响。
- 可再现性:指只要程序执行时的环境和初始条件相同,当程序重复执行时,不论它是从头到尾不停顿地执行,还是“走走停停”地执行,都可以获得相同的结果。这种特性,为程序员检测和校验程序的错误带来了很大的方便。
# 程序并发执行
程序顺序执行时,虽然可以给程序员带来方便,但系统资源的利用率却很低。为此,系统中引入了多道程序技术,使程序或程序段间能并发执行。然而,并非所有的程序都能发执行。
- 事实上,只有在不存在前趋关系的程序之间才有可能并发执行,否则无法并发执行
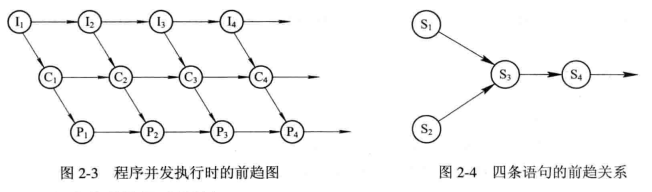
我们通过一个常见的例子来说明程序的顺序执行和并发执行。在图2-2中的输入程序、计算程序和打印程序三者之间,存在着Ii→Ci→Pi这样的前趋关系,以至对一个作业的输入、计算和打印三个程序段必须顺序执行。但若是对一批作业进行处理时,每道作业的输入、计算和打印程序段的执行情况如图2-3所示。输入程序(I1)在输入第一次数据后,由计算程序(C1)对该数据进行计算的同时,输入程序(I2)可再输入第二次数据,从而使第一个计算程序(C1)与第二个输入程序(I2)并发执行。事实上,正是由于C1和I1之间并不存在前趋关系,因此它们之间可以并发执行。一般来说,输入程序(Ii+1)在输入第i+1次数据时,计算程序(Ci)可能正在对程序(Ii)的第i次输入的数据进行计算,而打印程序(Pi-1)正在打印程序(Ci-1)的计算结果。 由图2-3可以看出,存在前趋关系Ii→Ci,Ii→Ii+1,Ci→Pi,Ci→Ci+1,Pi→Pi+1,而Ii+1和Ci,及Pi-1是重叠的,即在Pi-1和Ci,以及Ii+1之间,不存在前趋关系,可以并发执行。 对于具有下述四条语句的程序段:
S1: a:= x+2
S2: b:= y+4
S3: c:= a+b
S4: d:= c+b
可画出图2-4所示的前驱关系。可以看出,S3必须在a和b被赋值后方能执行;S4必须在S3之后执行;但S1和S2则可以并发执行,因为他们彼此互不依赖。
- 所以程序并发执行时有以下几个特征:
- 间断性。程序在并发执行时,由于它们共享系统资源,以及为完成同一项任务而相互合作,致使在这些并发执行的程序之间形成了相互制约的关系。例如,图2-3中的I、C和P是三个相互合作的程序,当计算程序完成Ci-1的计算后,如果输入程序Ii尚未完成数据的输入,则计算程序Ci就无法进行数据处理,必须暂停运行。只有当使程序暂停的因素消失后(如Ii已完成数据输入),计算程序Ci便可恢复执行。由此可见,相互制约将导致并发程序具有“执行—暂停—执行”这种间断性的活动规律。
- 失去封闭性。当系统中存在着多个可以并发执行的程序时,系统中的各种资源将为它们所共享,而这些资源的状态也由这些程序来改变,致使其中任一程序在运行时,其环境都必然会受到其它程序的影响。例如,当处理机已被分配给某个进程运行时,其它程序必须等待。显然,程序的运行已失去了封闭性。
- 不可再现性。程序在并发执行时,由于失去了封闭性,也将导致其又失去可再现性。例如,有两个循环程序A和B,它们共享一个变量N。程序A每执行一次时,都要做N=N+1操作;程序B每执行一次时,都要执行 Print(N) 操作,然后再将N置成“0”。程序A和B以不同的速度运行。这样,可能出现下述三种情况(假定某时刻变量N的值为n): ① N=N+1在Print(N)和N=0之前,此时得到的N值分别为n+1,n+1,0。 ② N=N+1在Print(N)和N=0之后,此时得到的N值分别为n,0,1。 ③ N=N+1在Print(N)和N=0之间,此时得到的N值分别为n,n+1,0。
- 上述情况说明,程序在并发执行时,由于失去了封闭性,其计算结果必将与并发程序的执行速度有关,从而使程序的执行失去了可再现性。换而言之,程序经过多次执行后,虽然它们执行时的环境和初始条件相同,但得到的结果却各不相同。
